This post explains how the key expansion process works for AES-128, AES-192, and AES-256.
To review some fundamentals: AES is an encryption standard that encrypts 128-bit blocks of plaintext into 128-bit blocks of ciphertext. The key size in AES is variable and can be 128, 192, or 256 bits.
Each round of encryption uses a unique subkey. The key expansion process is responsible for generating these subkeys for each round.
One common point of confusion is how AES can use keys longer than 128 bits when it operates on 128-bit blocks. The answer is straightforward: the operations are performed using 128-bit portions of the key at a time.
In AES-128, the 128-bit input key serves as the round 0 key, which is XORed with the initial state matrix. For subsequent rounds, different subkeys are generated from this input key through the key expansion process.
Working with “words” simplifies the understanding of the key scheduling dynamics. A “word” in this context refers to a 4-byte (32-bit) unit.
The AES 4×4 state matrix is composed of 4 words, with each word containing 4 bytes (4 x 8 bits = 32 bits).
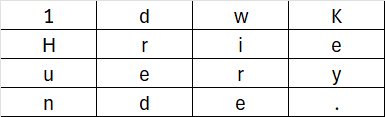
Each column in the key matrix represents a word. For example, the first column could be [ ‘1’, ‘H’, ‘u’, ‘n’ ], and these columns are often referred to as K0, K1, K2, K3.
For AES-128, the input key consists of 16 bytes (128 bits).
What about a key for AES-192? This key is longer—192 bits or 24 bytes.
Consider the key: '1HundredwireKeyForAES192'.
The number of rows in the state matrix is fixed at 4 (4 bytes per row), so each column forms a word of 32 bits. However, the number of columns in the matrix varies depending on the key length:
- For 256-bit keys, there are 8 columns.
- For 128-bit keys, there are 4 columns.
- For 192-bit keys, there are 6 columns.
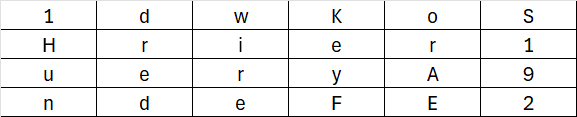
No matter the key size, the subkeys used during AES encryption are always 128 bits, meaning each subkey consists of 4 words (32 bits per word).
The input key provides a certain number of initial words. For example, in AES-192, the input key gives us 6 words: W0 to W5. These words can form the first subkey (W0 to W3), but we don’t have enough words to form subsequent subkeys. To address this, we need to expand the input key.
From here, we’ll focus on how to generate the expanded words. Once all the words are generated, we can group them into subkeys.
To explain the process, we’ll use a 192-bit key as an example. This key length is helpful for understanding how longer keys are converted into fixed 128-bit subkeys. The same principles apply to keys of 128 and 256 bits.
For AES-192, W4 and W5 come directly from the input key:
- W4 = [ ‘o’, ‘r’, ‘A’, ‘E’ ]
- W5 = [ ‘S’, ‘1’, ‘9’, ‘2’ ]
Now, let’s generate W6 using the steps of RotWord, SubWord, XOR with Rcon, and XOR with Wi-N:
- RotWord: Rotate the bytes in the word one position to the left.
- SubWord: Use the AES S-box to substitute each byte with its corresponding value, as in the encryption process.
- Rcon: XOR the first byte of the word with a round constant (Rcon), which varies for each round:
- Rcon = (0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8, 0xab, 0x4d, 0x9a)
- XOR with Wi-N: Perform a bitwise XOR with the word that is N positions before the current word (where N is the number of words in the key).
- For example, in AES-192, N = 6. If generating W6, XOR it with W0.
By following these steps, you can iteratively generate all the necessary words for key expansion.

For this round the Rcon is: [ ’01’, ’00’, ’00’, ’00’ ]
After performing the XOR operation with the output of SubWord, we get: [ ‘c6′, ’12’, ’23’, ‘ed’ ].
The final step is to XOR this result with Wi-N, where Wi-N in this case is W0.
After the XOR, we calculate: [ ‘f7’, ‘5a’, ’56’, ’83’ ].
With that, we have successfully generated a new word!
What about the next?
For the next word W7 the process is slightly different. Instead of using RotWord, SubWord, and Rcon, we simply XOR the previous word W6 with the Wi-N, which in this case is W1.
W7 = W6 XOR W2 = [ ’93’, ’28’, ’33’, ‘e7’ ]
Now we have two subkeys! The first is W0 to W3 which came directly from the input Key so
Subkey0: W0 = K0, W1 = K1, W2 = K21, W3 = K3
Subkey1: W4 = K4, W5 = K5, W6= [ ‘f7’, ‘5a’, ’56’, ’83’ ], W7 = [ ’93’, ’28’, ’33’, ‘e7’ ]
This process is the same for generating W7 through W11.
W12 undergoes the complete transformation RotWord, Subword, XOR Rcon, and XOR with Wi-N, just as we did for W6.
Perhaps you’re starting to notice a pattern. For a key length of 192 bits, which is composed of 6 words, every 6th word requires a full transformation. The other words are generated by simply performing a XOR operation between the previous word and Wi-N.
This pattern also holds true for a 128-bit key, which is composed of 4 words. Every 4th word requires a full transformation. The first 4 words of a 128-bit key are derived directly from the input key.
What about AES-256? Should I go for a full transformation every 8 words? Exactly! Every 8th round it undergoes a full transformation, and every 4th word undergoes a Subword transformation followed by a XOR with Wi-N. For all other words, it is simply a XOR operation withWi-N.
The image below, from Wikipedia, mathematically summarizes the rules it covers.
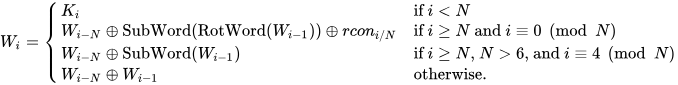
N is the number of words of the input key: 4 for AES-128, 6 for AES-192, 8 for AES-256.
Some examples:
- W7 for AES-256 for example, we will match the rule if i < 8 so we will use the K7 word.
- The next W8 would match the second rule, (if 8 >= 8 and 8 divided by 8 has remainder 0) which will make the full transformation to be applied Wi-N XOR with SubWord( RotWord( Wi-1 (previous word) )) XOR rcon.
- W9 won’t match any rule so we will perform Wi-N XOR Wi-1
Number of Subkeys generated:
- AES-128 goes for 10 rounds where it needs 11 subkeys ( 44 words);
- AES-192 goes for 12 rounds where it needs 13 subkeys (52 words);
- AES-256 goes for 14 rounds where it needs 15 subkeys (60 words);
All the logic implemented in the encryption is the same as I discussed in the previous topic. The only difference is that the encryption/decryption process has to go through extra rounds depending on the size of the key.
I have extended the previous code to support AES-128, AES-192, and AES-256 for study purposes only.
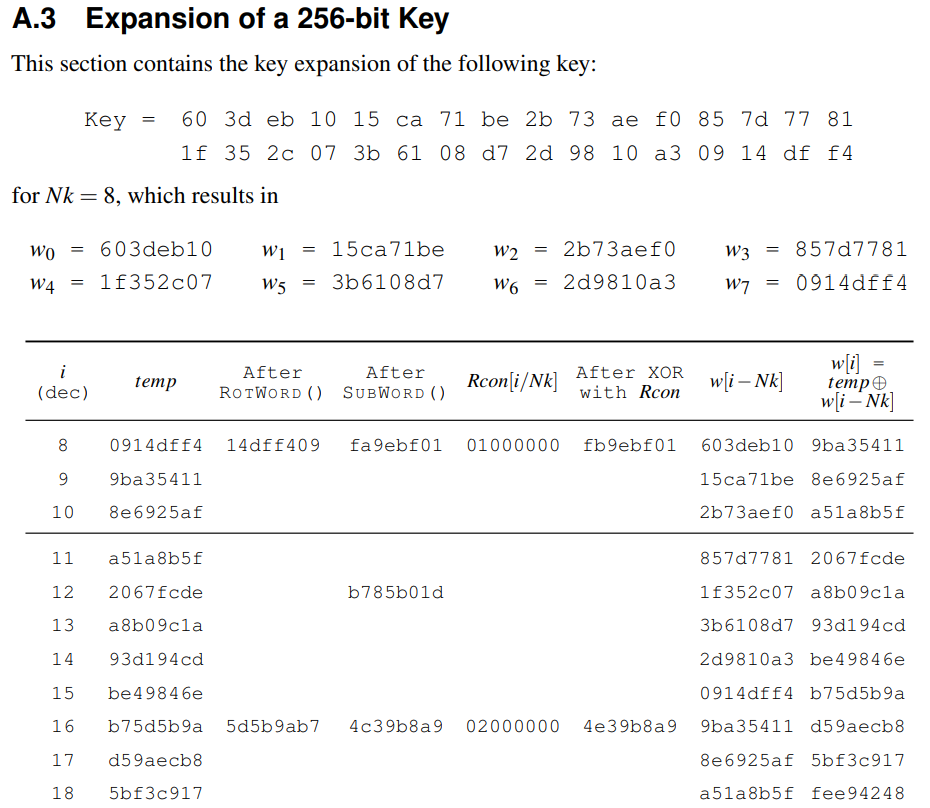
The NIST AES document contains examples that show the results of each transformation and step, which I found very useful.
Another awesome website is the https://legacy.cryptool.org/en/cto/aes-step-by-step here you can easily check the generated expasion keys, transformations, and more.
I hope I’ve been able to help you in some way.
Now that we know how to encrypt data, the next question is: how do we handle blocks larger than 128 bits? This is where encryption modes come in. In the next post, we’ll dive into the different modes and see how they let us work with larger blocks of data securely.
Just remember, the goal is to break down CCMP-AES (WPA2) piece by piece, and build a solid foundation for understanding the tech behind WPA3. Stay tuned, there’s more to come!
Github: https://github.com/dcapassi/py_AES
Thanks,
Diego Capassi
References
https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197-upd1.pdf
