In previous posts, we discussed how AES encryption works, breaking down the process of encrypting a 128-bit (16-byte) plaintext into a ciphertext of the same size. We also explained key expansion for 128, 192, and 256-bit keys, detailing how the subkeys used in the AES algorithm are generated.

The goal is to gain a deep understanding of how CCMP works, dissecting it piece by piece to fully comprehend it later.

Now, let’s say we want to encrypt the message: “1HundredWire has some cool content”. This message contains 34 characters, each mapped to a single byte, resulting in 34 bytes. Since AES encrypts 16 bytes of plaintext into 16 bytes of ciphertext, how can we handle a message longer than 16 bytes?

Padding

A straightforward approach would be to split the plaintext message into 16-byte blocks and encrypt each block.

Looking at block 3, we notice that from byte 3 to 16, there are no values. This means we’ll need to add some padding!

Many implementations use the padding standard defined in RFC 2315 (PKCS #7).

To apply this padding, we split the data into blocks of size N (in this case, N = 16) and check the length (L) of the last block.

In the example above, L is 2, meaning we are missing 14 bytes to complete the block (N – L).

The value 14 in hexadecimal is 0x0e, so we append 0x0e to the message repeatedly until the block is filled.

If the last block had a length (L) of 16, meaning it is already complete, we would add an additional block filled entirely with 0x10. This is because PKCS#7 always adds padding to the message, even if the last block is already full.

Now, let’s encrypt it!

ECB

A straightforward approach is to encrypt each block separately and then append them to form a single ciphertext. This method is known as ECB (Electronic Codebook) mode. See the diagram below:

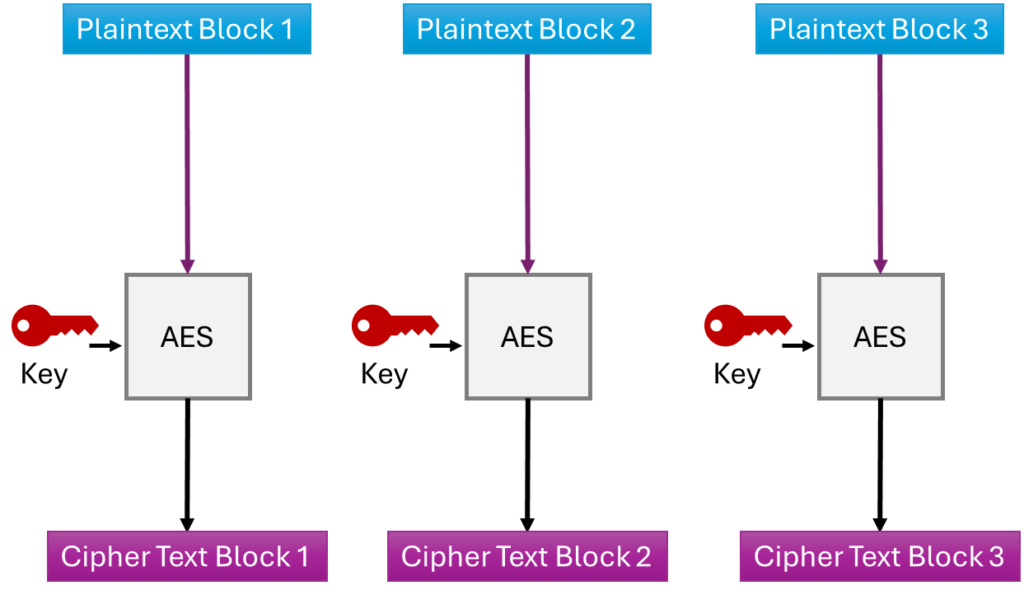
For this example, we’ll use a 256-bit key: ‘this_is_a_256b_key_wich_has_32B!’

Next, we’ll obtain the cipher blocks:

This process results in a ciphertext formed by appending the encrypted blocks together:

Ciphertext in Hex: d25f93720e3802ee2e1eafe82fb07e95712bd63011e949fbde2abf6e10c62edef632e785205cc11e12904a0388b7faa3

This method is straightforward to implement and can be parallelized since each block can be encrypted or decrypted independently without requiring additional information.

However, there’s a significant problem: what happens if the same data appears in multiple blocks?
The answer: each block will produce the exact same ciphertext. This can reveal patterns in the message, compromising security.

In ECB mode, identical plaintext blocks will always result in identical ciphertext blocks because there is no chaining between blocks.

A classic example is encrypting an image of the Linux mascot, Tux, using ECB mode. Patterns in the image remain visible, highlighting the flaw of this method.

Each pixel’s RGB value is encrypted individually

We can clearly identify that it’s an image of a penguin.

CBC

ECB is not considered a secure encryption mode, as patterns in the data can be easily recognized, depending on the type of data being encrypted.

A better approach would be CBC (Cipher Block Chaining). The idea is to use the output of one block to modify the input of the next block through the XOR operation. For the first block, the XOR operation is performed between the plaintext and an Initialization Vector (IV).

The diagram below summarizes the process:

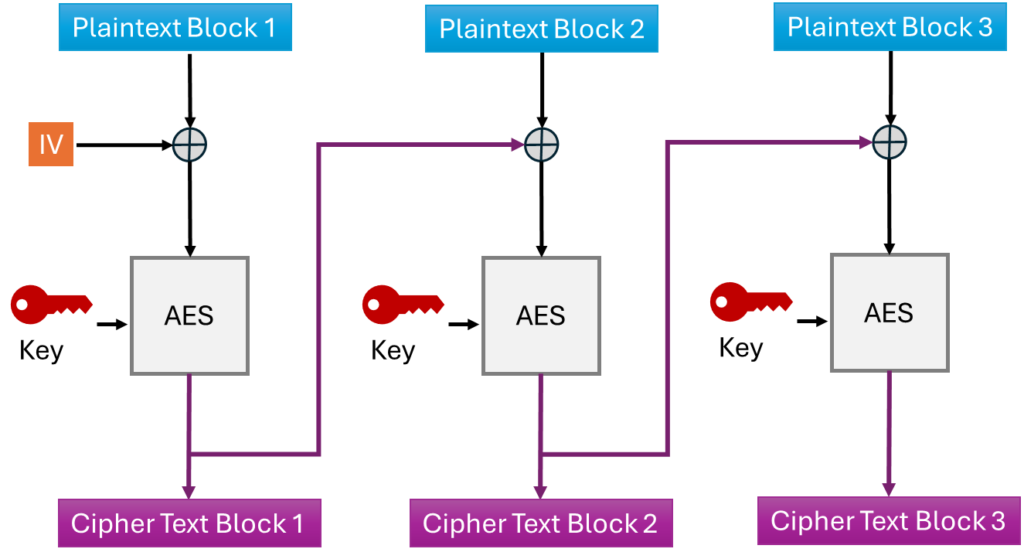
This approach solves the pattern recognition problem of ECB. Even if the same plaintext block is repeated, each ciphertext block will be different due to the use of the Initialization Vector (IV).

Let’s check what the output would look like using the same scenario, with the IV: ‘random_123456789’.

block1 = 7bddbb547a5d2239c3642b9f633c9e5c

block2 = 43cc1f3be857ea5ed8de1a439b5d7357

block3 = 80a652f43548cc16d911de8488ad2a87

Resulting in the ciphertext 7bddbb547a5d2239c3642b9f633c9e5c43cc1f3be857ea5ed8de1a439b5d735780a652f43548cc16d911de8488ad2a87

To decrypt the ciphertext, the process follows the diagram below:

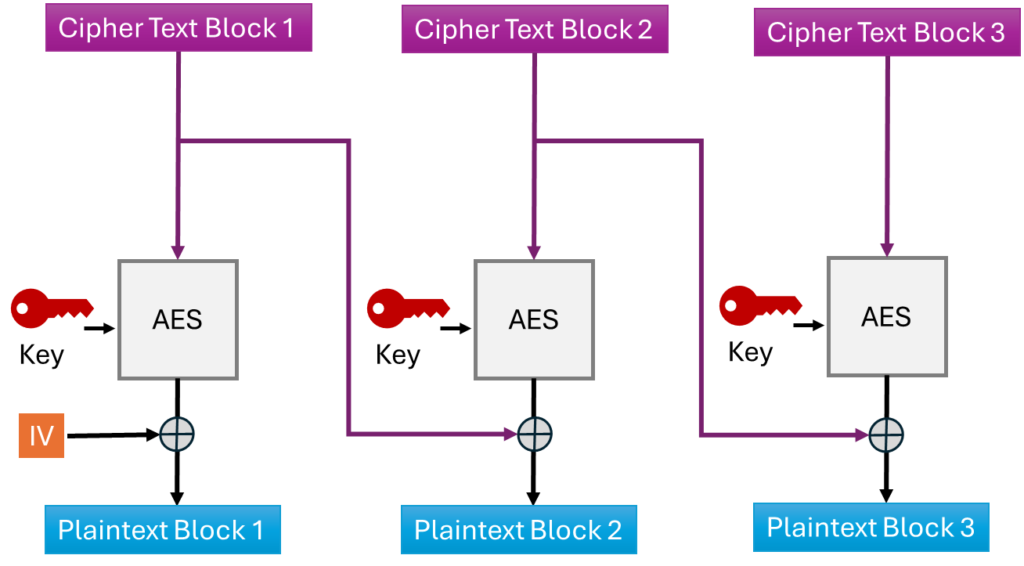
To decrypt, the process follows these steps:

• Ciphertext block 1 is decrypted and XORed with the IV.
• The output of the first block is then XORed with Ciphertext block 2.
• Finally, Ciphertext block 3 is decrypted and XORed with Ciphertext block 2.

Let’s change the plaintext to:
“123456789abcdefg________________123456789abcdefg”
This consists of two 16-byte blocks with the same data, separated by a block of white spaces.

With ECB, the output ciphertext is:

92DF918A6538DEC50A6D41C30647732129A34FB529CCCE4F5EEDE37326D7A9E992DF918A6538DEC50A6D41C306477321DCDC6ACD066221CA558C0846B41FB47B

In ECB mode, the yellow parts of the ciphertext are identical, and the last block is the padding. An attacker examining the ciphertext would notice that two blocks are the same, which reveals information about the structure of the plaintext.

Now, let’s see the same message encrypted using CBC:

3E276E10B26EB7AEAD516ED2D2FE643C867CE8D7945BA88F0B74BA38FCC4DF48F671D190307715F2F3430D28C8AD469E11CC881F7A4FC2DF75248545208C0EE5

By comparing the first 32 bytes and the third 32-byte blocks, we can no longer detect any patterns.

The drawback of this method is that it cannot be performed in parallel since the output of each block depends on the output of the previous block. It also requires an Initialization Vector (IV), which must be known by both peers in the communication. The application must ensure that the IV is not reused to avoid situations where identical plaintext blocks result in the same ciphertext, allowing an attacker to guess the plaintext.

CTR

The last encryption mode discussed in this post is CTR (Counter mode). In this mode, AES encrypts a 128-bit counter instead of the plaintext. This creates a 128-bit ciphertext, which is then XORed with the plaintext. The interesting aspect of CTR is that there’s no need to split the plaintext into 128-bit blocks. If the message is shorter than 128 bits, the ciphertext is truncated to match the length of the plaintext and then XORed. In this case, the encryption mode behaves more like a stream cipher rather than a block cipher!

The diagram below illustrates how CTR works:

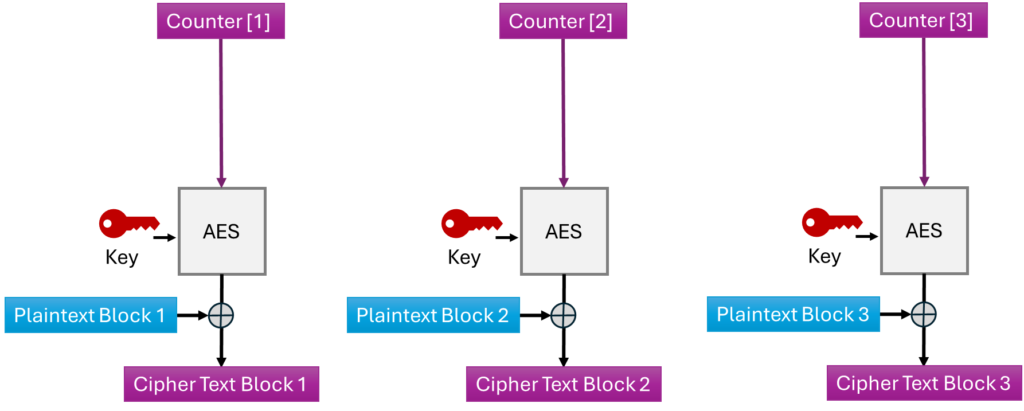
This approach solves the pattern recognition problem, as the counter must be unique for each encryption. It also addresses the issue of serialization, as either the receiver or transmitter can calculate the counter to encrypt or decrypt the message.

The decryption process is straightforward: it follows the same process as encryption by encrypting the counter, but instead of XORing with the plaintext, it XORs with the ciphertext.

The drawback of this method is that it is susceptible to bit-flipping attacks. If an attacker changes a single bit of the ciphertext, only a single bit of the decrypted plaintext will be affected. In contrast, a bit-flip in CBC or ECB would change the entire block of plaintext.

This implementation requires careful management of the Nonce, which serves as the base value that is incremented and must be unique.

Let’s create a simple example with the message:
‘IPv4 Address – Default Gateway:10.1.1.1’
This message is 39 bytes long. Since CTR is a stream cipher, there’s no need to pad the message. The first step is to create blocks of 16 bytes:

The cipher text will be: 136A096685AB2DCCC3C231382D52BAA497B3EA24C8F67A38D3513D762DC517AEECA1143A6FE980

The last byte (0x80) is related to the final byte of the plaintext message (1).

Now, let’s consider what happens if an attacker changes the ciphertext during transit. Let’s change the byte from 0x80 to 0x82 and observe the result:

The decrypted message now becomes:
‘IPv4 Address – Default Gateway:10.1.1.3’
This could be part of a man-in-the-middle attack, where an attacker intercepts and modifies the ciphertext.

To mitigate this, encryption modes like CTR should be used alongside methods to authenticate the message and ensure it hasn’t been tampered with. This is precisely what Counter with CBC-MAC (CCM) and Galois Counter Mode (GCM) achieve. Both of these methods add authentication to the message, using CTR as the base for encryption.

For example, WPA2 uses AES-CCMP, which relies on AES in CTR mode, while WPA3 utilizes AES-GCM for encryption.

In the next post, I will explain how CBC-MAC works, along with some real test vectors as examples!

Stay tuned,

Diego Capassi