One of my favorite acronyms in the industry is CCMP-AES. It’s quite a mouthful: Counter Mode Cipher Block Chaining Message Authentication Code Protocol with Advanced Encryption Standard. Isn’t that cool?

For those looking for context, CCMP-AES is one of the security mechanisms defined in the 802.11i (RSN) standard. It provides a secure way for devices to send encrypted, authenticated traffic while ensuring data integrity.

Here are the key components:

• AES (Advanced Encryption Standard)
• Counter Mode
• Cipher Block Chaining
• Message Authentication Code

There’s plenty of information online, but my goal is to break it down into smaller, digestible chunks. Eventually, I aim to write code that interacts with real network devices, enabling encrypted communication both ways. Let’s start with AES, this post will talk about the encryption process, getting a little deeper in the steps involved.

AES

History

In 1997, the National Institute of Standards and Technology (NIST) in the United States announced its search for a successor to the Data Encryption Standard (DES). The requirements were clear: the new algorithm needed to be a symmetric block cipher, implementable in both hardware and software. Interestingly, the name “Advanced Encryption Standard” (AES) was already defined in the announcement document, titled “Announcing Development of a Federal Information Processing Standard for Advanced Encryption Standard” (NIST Announcement).

The algorithm Rijndael, developed by Belgian cryptographers Joan Daemen and Vincent Rijmen, won the competition. In 2001, it was formally adopted as the encryption standard AES (FIPS PUB 197) (FIPS PUB 197).

Basics

So, what is AES used for? AES is an encryption standard that converts blocks of plaintext into ciphertext. It uses a subkey the same length as the block of data to be encrypted (128 bits). AES supports key lengths of 128, 192, and 256 bits, but the block size is fixed at 128 bits.

To better understand AES encryption, let’s break down the steps of the AES-128 process. Keep in mind that the key schedule slightly differs for AES-192 and AES-256.

The following diagram summarizes the AES-128 encryption blocks:

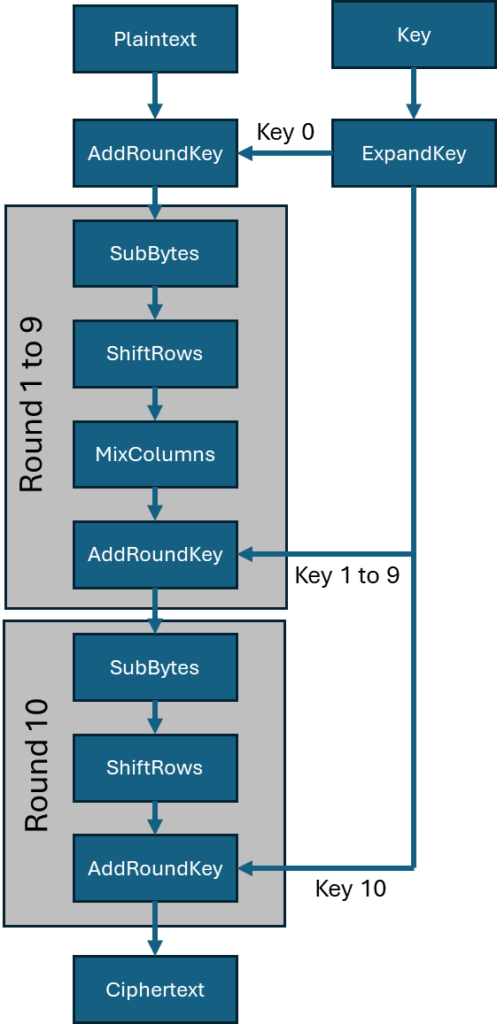
Key Expansion

AES begins with a key expansion algorithm, which generates a series of 128-bit subkeys from the initial input key. These subkeys are used in different rounds of encryption.

Initial Transformation

The plaintext and the input key are each converted into a matrix format, known as the state matrix, which is a 4×4 grid. Before proceeding with further transformations, a bitwise XOR operation is performed between the plaintext matrix and the key matrix.

Here is the initial setup for this example:

• Key: 1HundredwireKey
• Plaintext: 1HundredwireWiFi

Matrix Conversion

Both the key and plaintext are represented as a 4×4 matrix:

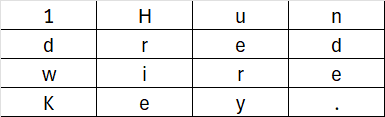
The format which is the AES algorithm works is transposed, so each column will represent a row.

The AES algorithm uses a transposed format, where each column in the state matrix represents a row of the input data.

Before entering the round loop, an AddRoundKey operation is performed. This involves a XOR operation between the plaintext matrix and the key matrix.

XOR (exclusive-OR) is a bitwise operation that works as follows

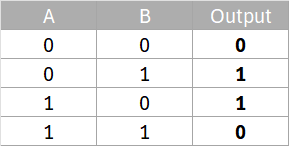
For example, the element (6E) at position [0][3] in the Key Matrix will be XORed with the element at position [0][3] in the Text Matrix, which is also (6E).

• Key Matrix [0][3]: 6E (HEX) → 1101110 (BIN)
• Text Matrix [0][3]: 6E (HEX) → 1101110 (BIN)

The XOR result is 0x00, as XOR-ing identical binary values results in zero.

In this example, the key and text matrices share identical bytes except for the last four. This similarity results in a large number of zeros during the first AddRoundKey operation.

Now, let’s perform the XOR operation on the last column, where the bytes differ:

• Key Matrix [3][0]: 4B (HEX) → 01001011 (BIN)
• Text Matrix [3][0]: 57 (HEX) → 01010111 (BIN)

The XOR result for these differing bytes will showcase a non-zero output, highlighting the changes introduced by the key.

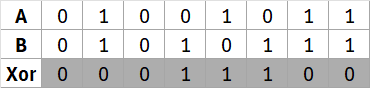
The XOR will be 1C.

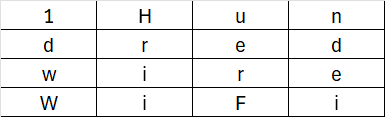
The AddRoundKey will result in:

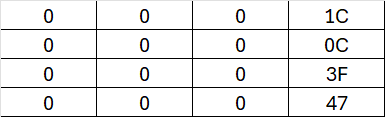
Now, this matrix (referred to as the State) will undergo several rounds, during which four transformations are applied.

The first transformation is SubBytes, which is straightforward: each byte in the State is replaced using a predefined lookup table called the S-box. This substitution is performed byte-by-byte, based on the values specified in the S-box.

Below is an image from the NIST AES standard that illustrates the S-box.

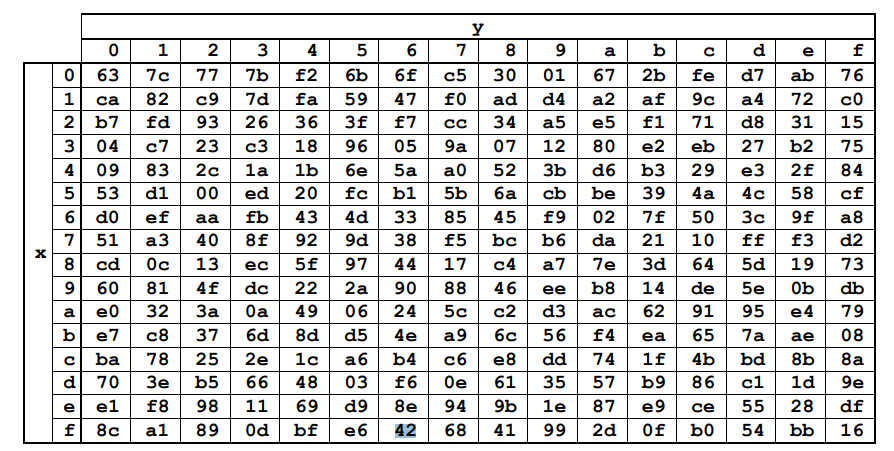
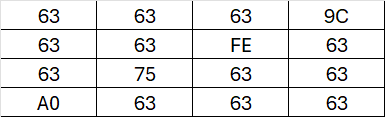
After applying the SubBytes operation to our table, we end up with numerous 63s due to the presence of many 0s

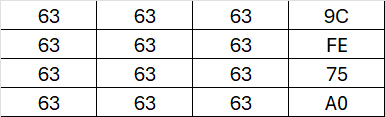
At this point, our State is still not well mixed, and it even reveals that we’ve chosen a key that is somewhat similar to the text we want to encrypt.

Now, let’s move on to the next step of the round:

ShiftRows

This transformation cyclically shifts the values of the rows. The first row remains unchanged, while the other rows are shifted to the left by 1, 2, and 3 positions, respectively.

Since we have many identical values, it may be difficult to observe the effect of each individual byte. Let’s look at the example below:

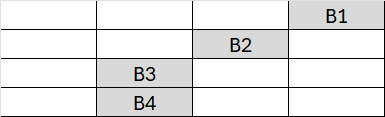
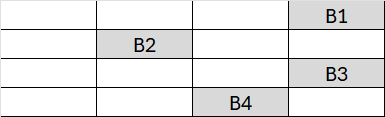
The state Matrix will be:

So far, I’ve left out an important detail: all of AES operates using elements from a finite field, where addition and multiplication follow different rules compared to regular numbers. I won’t dive into the details of finite fields here, but it’s important to note that AES uses the finite field GF(2^8).

In this field, both addition and subtraction are equivalent to XOR operations.

Hex 63 in binary is (01100011) in the polynomial notation is x⁶+x⁵+x+1.

Let’s do the multiplication of 63 with 02 (00000010)

2 in polynomial format is x

(x⁶+x⁵+x+1)*(x)

The result is (x⁷+x⁶+x²+x) which is good because it inside the finite field of GF(2⁸) where the max element is

x⁷+ x⁶+x⁵+x⁴+x³+x²+x+1.

(x⁷+x⁶+x²+x) in binary is 11000110 in hex is C6

But, what if we multiple it by 2 again?

(x⁷+x⁶+x²+x) * x = (x⁸+x⁷+x⁶+x²)

Now we have a problem, this element is not part of the finite field GF(2⁸). We have to perform the modulo operation using a irreducible polynomial for the AES algorithm the polynomial is x⁸+x⁴+x³+x+1.

(x⁸+x⁷+x⁶+x²) modulo x⁸+x⁴+x³+x+1 equals x⁷+x⁴+x²+x+1 in binary it is 10010111 and hex 97.

Returning to AES, the MixColumns operation is applied to the State matrix.

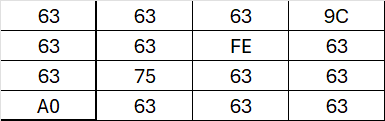
We take the first column of the State matrix and multiply each element by the corresponding element in the multiplication matrix. This procedure is repeated for every column of the State matrix.

As an example, let’s calculate the last item of the first column in the MixColumns operation. It’s calculated as:

(63 * 03) ⊕ (63 * 01) ⊕ (63 * 01) ⊕ (A0 * 02).

The polynomial for of each element is

01 is 1,

02 is x

03 is x+1

A0 is x⁷+x⁵

63 is x⁶+x⁵+x+1

63 * 03 = (x⁶+x⁵+x+1)(x+1) = x⁷+x⁵+x²+1

63 * 01 = (x⁶+x⁵+x+1)

A0 * 02 = (x⁷+x⁵)(x) = x⁶+x⁴+x³+x+1

Let’s XOR

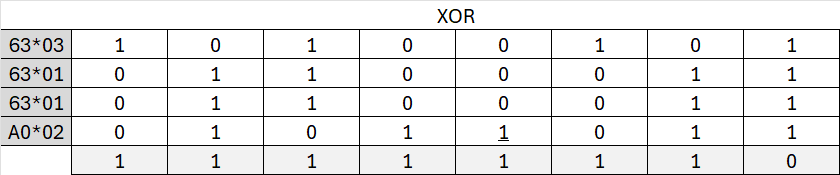
The result of the XOR is 253 (FE)

After doing the whole mix column process we get:

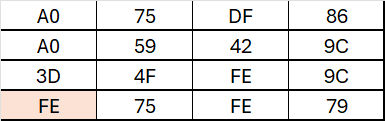
The next step after finishing the MixColumn is the AddRoundKey which is a XOR operation between the state matrix and round key. On this post i will not explain how the keys are generated but for each round a different key is used.

The first Round key is:

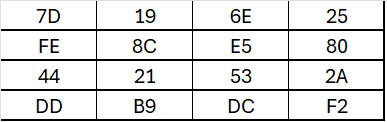
After performing the XOR operation with this, we will obtain:

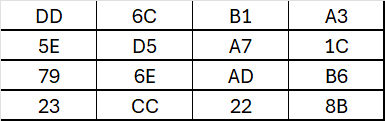
This process is repeated 9 times for AES-128.

Afterward, the final round involves SubBytes, ShiftRows, and AddRoundKey using the last round key.

The image below summarizes the steps used in the encryption process, as outlined in the NIST AES specification.

At the end of the process, the expected ciphertext is: 6d8b1121c2ba4cd539b11712bc39eb87.

In the next post, I will explain the Key Expansion algorithm and walk through some decryption steps.

I’ve developed a simple implementation of AES-128 in Python. You can check it out to learn more about the implementation details: https://github.com/dcapassi/python_AES-128

In summary, AES encryption operates in the finite field known as Galois Field GF(2^8). With a series of relatively simple operations, it is possible to create a robust cipher.

Thanks,

Diego Capassi

References
Advanced Encryption Standard (AES) FIPS-197 – https://doi.org/10.6028/NIST.FIPS.197-upd1