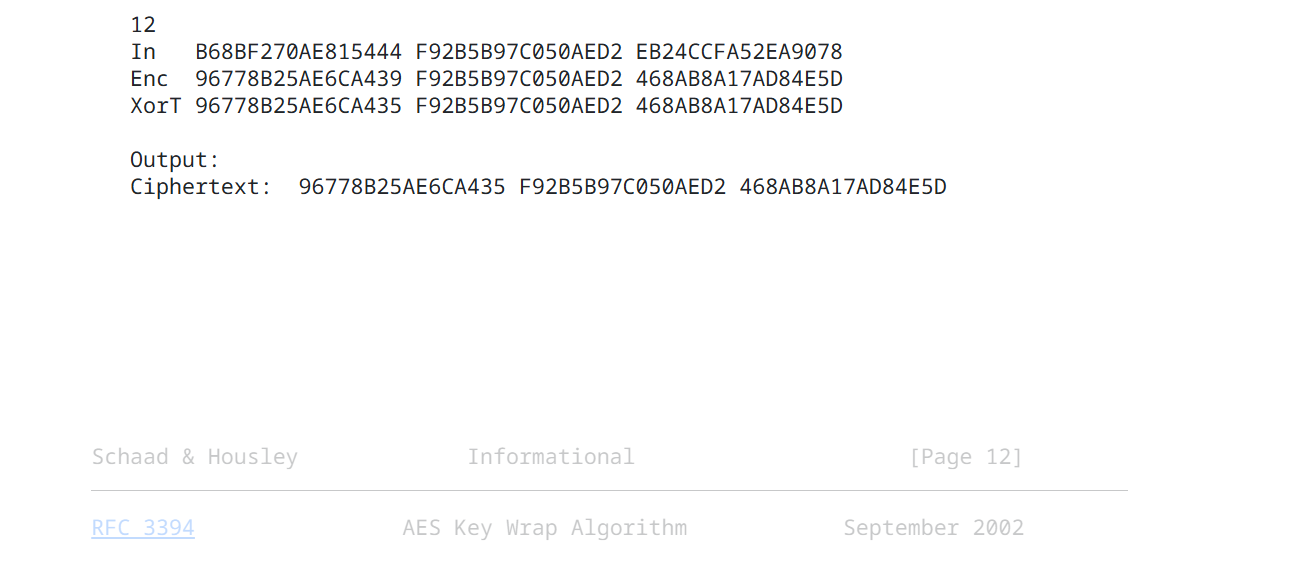
When we need to securely send a key, we encrypt it. That’s exactly what AES Key Wrap does—it provides a standardized way to encrypt a key for safe transport.
AES Key Wrap uses a Key Encryption Key (KEK) to encrypt the key we want to protect. It applies the AES algorithm to 64-bit blocks, producing a ciphertext that securely contains the key. This process also includes an integrity check to ensure the ciphertext hasn’t been tampered with.
The algorithm follows standards set by NIST (National Institute of Standards and Technology) and is detailed in RFC 3394. It works by dividing the input data into 64-bit blocks and encrypting them.
AES Key Wrap supports AES key lengths of 128, 192, or 256 bits, allowing for different levels of security.
How Does It Work?
There are three phases: initializing variables, calculating intermediate values, and outputting results.
Initialize Variables
The register used for integrity checking (A) receives the initial value: 0xA6A6A6A6A6A6A6A6.
The variable R, which will undergo transformations, receives the plaintext blocks of 64 bits each.
These blocks can be accessed as R[i], where i ranges from 1 to n.
Calculate Intermediate Values
There are two loops: the outer loop runs from j = 0 to 5, and the inner loop runs from i = 1 to n.
For each cycle, B is calculated by running the AES encryption using the KEK as the key and the message as A concatenated with R[i].
AES( KEK, A | R[i] )
A is updated to the 64 most significant bits of B, XORed with t, where t = (n * j) + i (encoded in 64 bits).
Finally, R[i] receives the last 64 bits (LSB) of B.
This process is repeated for each block (n) over six cycles (j).
Output Results
The ciphertext C[0] receives the integrity check value (A), and C[i] (for i = 1 to n) receives R[i].
Key Unwrap
To reverse the process, the inputs are the ciphertext (C), the key (KEK), and the output is the plaintext (P).
Initialize Variables
A = C[0]
The variable R receives the ciphertext blocks of 64 bits each:
R[i] = C[i] for i = 1 to n.
Compute Intermediate Values
There are two loops: the outer loop runs from j = 5 to 0, and the inner loop runs from i = n to 1.
The core operation calculates B using AES decryption with the KEK and the message (A ^ t) | R[i], where t = (n * j) + i (encoded in 64 bits).
A is updated to the 64 most significant bits of B.
R[i] receives the last 64 bits of B.
Output Results
A is checked against the IV 0xA6A6A6A6A6A6A6A6. If it does not match, the function must return an error.
If the integrity check (A) matches the IV, the key unwrap function returns the plaintext: P[i] = R[i].
Key Wrap – Test Vector Example
Let’s walk through some steps of the AES key wrap algorithm using the test vector from the RFC 3394.
plaintext/key data (P): 00112233445566778899AABBCCDDEEFF
KEK (K): 000102030405060708090A0B0C0D0E0F1011121314151617
A begins with the IV = 0xA6A6A6A6A6A6A6A6
R = P
P has 128 bits, so it is divided in two blocks of 64 bits = [ [‘0011223344556677’],[‘8899AABBCCDDEEFF’] ]
Iteration j=0 and i=1
B = AES(K, A6A6A6A6A6A6A6A60011223344556677)
B = 0xdfe8fd5d1a3786a7351d385096ccfb29
t = (n * j) + i = 2 * 0 + 1 = 1
A = 0xdfe8fd5d1a3786a7 ⊕ 0x0000000000000001
A = 0xdfe8fd5d1a3786a6
R[1] = 0x351d385096ccfb29
R[2] is 0x8899AABBCCDDEEFF (was not changed)
Iteration j=0 and i=2
B = AES(K, A | R[i] ) = 0x9d9b32b9ed742e0251f22f3286758a2d
t = (n * j) + i = 2 * 0 + 2 = 2
A = 0x9d9b32b9ed742e02 ⊕ 0x0000000000000002 = 0x9d9b32b9ed742e00
R[1] = 0x351d385096ccfb29 (was not changed)
R[2] = 0x51f22f3286758a2d
Iteration j=1 and i=1
B = AES(K, A | R[i] ) = 0x7b8e343ca51cf8abbc164f51e20cc983
t = (n * j) + i = 2 * 1 + 1 = 3
A = 0x7b8e343ca51cf8ab ⊕ 0x0000000000000003 = 0x7b8e343ca51cf8a8
R[1] = 0xbc164f51e20cc983
R[2] = 0x51f22f3286758a2d (was not changed)
Iteration j=1 and i=2
B = AES(K, A | R[i] ) = 0x02a97c589714059505fc2d8f8ff4b919
t = (n * j) + i = 2 * 1 + 2 = 4
A = 0x02a97c5897140595 ⊕ 0x0000000000000004 = 0x02a97c5897140591
R[1] = 0xbc164f51e20cc983 (was not changed)
R[2] = 0x05fc2d8f8ff4b919
Iteration j=2 and i=1
B = AES(K, A | R[i] ) = 0x15d4b63f66583817429487269d3a0016
t = (n * j) + i = 2 * 2 + 1 = 5
A = 15d4b63f66583817 ⊕ 0x0000000000000005 = 0x15d4b63f66583812
R[1] = 0x429487269d3a0016
R[2] = 0x05fc2d8f8ff4b919 (was not changed)
Iteration j=2 and i=2
B = AES(K, A | R[i] ) = 0xae2d0b76a6951eea05a2d8fb4dd5bd7a
t = (n * j) + i = 2 * 2 + 2 = 6
A = 0xae2d0b76a6951eea ⊕ 0x0000000000000006 = 0xae2d0b76a6951eec
R[1] = 0x429487269d3a0016 (was not changed)
R[2] = 0x05a2d8fb4dd5bd7a
Iteration j=3 and i=1
B = AES(K, A | R[i] ) = 0x79f849444f4b8aa8d40b091cdbac0340
t = (n * j) + i = 2 * 3 + 1 = 7
A = 0x79f849444f4b8aa8 ⊕ 0x0000000000000007 = 0x79f849444f4b8aaf
R[1] = 0xd40b091cdbac0340
R[2] = 0x05a2d8fb4dd5bd7a (was not changed)
Iteration j=3 and i=2
B = AES(K, A | R[i] ) = 0x5933a9195b5f5e2189f0d6c06f8ca9b4
t = (n * j) + i = 2 * 3 + 2 = 8
A = 0x5933a9195b5f5e21⊕ 0x0000000000000008 = 0x5933a9195b5f5e29
R[1] = 0xd40b091cdbac0340 (was not changed)
R[2] = 0x89f0d6c06f8ca9b4
Iteration j=4 and i=1
B = AES(K, A | R[i] ) = 0x57ada800299c2e854d5b3dfe7c04abba
t = (n * j) + i = 2 * 4 + 1 = 9
A = 0x57ada800299c2e85⊕ 0x0000000000000009 = 0x57ada800299c2e8c
R[1] = 0x4d5b3dfe7c04abba
R[2] = 0x89f0d6c06f8ca9b4 (was not changed)
Iteration j=4 and i=2
B = AES(K, A | R[i] ) = 0xbf17bd6a9bc80163eb24ccfa52ea9078
t = (n * j) + i = 2 * 4 + 2 = 10
A = 0xbf17bd6a9bc80163 ⊕ 0x000000000000000A = 0xbf17bd6a9bc80169
R[1] = 0x4d5b3dfe7c04abba (was not changed)
R[2] = 0xeb24ccfa52ea9078
Iteration j=5 and i=1
B = AES(K, A | R[i] ) = 0xb68bf270ae81544ff92b5b97c050aed2
t = (n * j) + i = 2 * 4 + 1 = 11
A = 0xb68bf270ae81544f ⊕ 0x000000000000000B = 0xb68bf270ae815444
R[1] = 0xf92b5b97c050aed2
R[2] = 0xeb24ccfa52ea9078 (was not changed)
Iteration j=6 and i=2
B = AES(K, A | R[i] ) = 0x96778b25ae6ca439468ab8a17ad84e5d
t = (n * j) + i = 2 * 4 + 1 = 12
A = 0x96778b25ae6ca439 ⊕ 0x000000000000000C = 0x96778b25ae6ca435
R[1] = 0xf92b5b97c050aed2 (was not changed)
R[2] = 0x468ab8a17ad84e5d
Output results
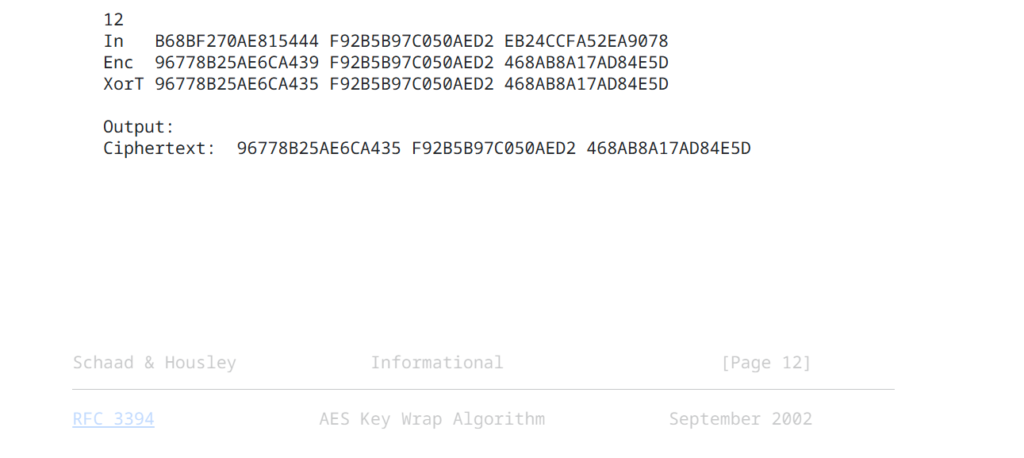
The ouput C is A concatenated with R[1] and R[2] which is 0x96778b25ae6ca435f92b5b97c050aed2468ab8a17ad84e5d.
Key Unwrap – Test Vector Example
Now, let’s reverse the process by unwrapping the output from the previous example.
At the end of the operation, the calculated integrity field should match the IV: 0xA6A6A6A6A6A6A6A6
C = 0x96778b25ae6ca435f92b5b97c050aed2468ab8a17ad84e5d
C divided in 64 bits blocks = [[‘0x96778b25ae6ca435’],[‘0xf92b5b97c050aed2’],[‘0x468ab8a17ad84e5d’]]
A = C[1] = 0x96778b25ae6ca435
R = [ C[2] , C[3] ] = [[‘0xf92b5b97c050aed2’],[‘0x468ab8a17ad84e5d’]]
Iteration j=5 and i=2
t = (n * j) + i = 2 * 5 + 2 = 12
A ⊕ t = 0x96778b25ae6ca435 ⊕ 0x000000000000000C = 0x96778b25ae6ca439
B = AES-1(K, (A ⊕ t) | R[i] ) = 0xb68bf270ae815444eb24ccfa52ea9078
A = 0xb68bf270ae815444
R[1] = 0xf92b5b97c050aed2 (was not changed)
R[2] = 0xeb24ccfa52ea9078
Iteration j=5 and i=1
t = (n * j) + i = 2 * 5 + 1 = 11
A ⊕ t = 0xb68bf270ae815444 ⊕ 0x000000000000000B = 0xb68bf270ae81544f
B = AES-1(K, (A ⊕ t) | R[i] ) = 0xbf17bd6a9bc801694d5b3dfe7c04abba
A = 0xbf17bd6a9bc80169
R[1] = 0x4d5b3dfe7c04abba
R[2] = 0xeb24ccfa52ea9078 (was not changed)
Iteration j=4 and i=2
t = (n * j) + i = 2 * 4 + 2 = 10
A ⊕ t = 0xbf17bd6a9bc80169 ⊕ 0x000000000000000A = 0xbf17bd6a9bc80163
B = AES-1(K, (A ⊕ t) | R[i] ) = 0x57ada800299c2e8c89f0d6c06f8ca9b4
A = 0x57ada800299c2e8c
R[1] = 0x4d5b3dfe7c04abba (was not changed)
R[2] = 0x89f0d6c06f8ca9b4
Iteration j=3 and i=2
t = (n * j) + i = 2 * 3 + 2 = 8
A ⊕ t = 0x5933a9195b5f5e29 ⊕ 0x0000000000000008 = 0x5933a9195b5f5e21
B = AES-1(K, (A ⊕ t) | R[i] ) = 0x79f849444f4b8aaf05a2d8fb4dd5bd7a
A = 0x79f849444f4b8aaf
R[1] = 0xd40b091cdbac0340 (was not changed)
R[2] = 0x05a2d8fb4dd5bd7a
Iteration j=3 and i=1
t = (n * j) + i = 2 * 3 + 1 = 7
A ⊕ t = 0x79f849444f4b8aaf ⊕ 0x0000000000000007 = 0x79f849444f4b8aa8
B = AES-1(K, (A ⊕ t) | R[i] ) = 0xae2d0b76a6951eec429487269d3a0016
A = 0xae2d0b76a6951eec
R[1] = 0x429487269d3a0016
R[2] = 0x05a2d8fb4dd5bd7a (was not changed)
Iteration j=2 and i=2
t = (n * j) + i = 2 * 2 + 2 = 6
A ⊕ t = 0xae2d0b76a6951eec ⊕ 0x0000000000000006 = 0xae2d0b76a6951eea
B = AES-1(K, (A ⊕ t) | R[i] ) = 0x15d4b63f6658381205fc2d8f8ff4b919
A = 0x15d4b63f66583812
R[1] = 0x429487269d3a0016 (was not changed)
R[2] = 0x05fc2d8f8ff4b919
Iteration j=2 and i=1
t = (n * j) + i = 2 * 2 + 1 = 5
A ⊕ t = 0x15d4b63f66583812 ⊕ 0x0000000000000005 = 0x02a97c5897140591bc164f51e20cc983
B = AES-1(K, (A ⊕ t) | R[i] ) =
A = 0x02a97c5897140591
R[1] = 0xbc164f51e20cc983
R[2] = 0x05fc2d8f8ff4b919 (was not changed)
Iteration j=1 and i=2
t = (n * j) + i = 2 * 1 + 2 = 4
A ⊕ t = 0x02a97c5897140591⊕ 0x0000000000000004 = 0x02a97c5897140595
B = AES-1(K, (A ⊕ t) | R[i] ) = 0x7b8e343ca51cf8a851f22f3286758a2d
A = 0x7b8e343ca51cf8a8
R[1] = 0xbc164f51e20cc983 (was not changed)
R[2] = 0x51f22f3286758a2d
Iteration j=1 and i=1
t = (n * j) + i = 2 * 1 + 1 = 3
A ⊕ t = 0x7b8e343ca51cf8a8 ⊕ 0x0000000000000003 = 0x7b8e343ca51cf8ab
B = AES-1(K, (A ⊕ t) | R[i] ) = 9d9b32b9ed742e00351d385096ccfb29
A = 0x9d9b32b9ed742e00
R[1] = 0x351d385096ccfb29
R[2] = 0x51f22f3286758a2d (was not changed)
Iteration j=0 and i=2
t = (n * j) + i = 2 * 0 + 2 = 2
A ⊕ t = 0x9d9b32b9ed742e00 ⊕ 0x0000000000000002 = 0x9d9b32b9ed742e02
B = AES-1(K, (A ⊕ t) | R[i] ) = 0xdfe8fd5d1a3786a68899aabbccddeeff
A = 0xdfe8fd5d1a3786a6
R[1] = 0x351d385096ccfb29 (was not changed)
R[2] = 0x8899aabbccddeeff
Iteration j=0 and i=1
t = (n * j) + i = 2 * 0 + 1 = 1
A ⊕ t = 0xdfe8fd5d1a3786a6 ⊕ 0x0000000000000001 = 0xdfe8fd5d1a3786a7
B = AES-1(K, (A ⊕ t) | R[i] ) = 0xa6a6a6a6a6a6a6a60011223344556677
A = 0xa6a6a6a6a6a6a6a6
R[1] = 0x0011223344556677
R[2] = 0x8899aabbccddeeff (was not changed)
As expected the integrity check value is ‘0xa6a6a6a6a6a6a6a6’, the output plaintext P is R[1] concatenated with R[2], resulting in:
P = 0x00112233445566778899aabbccddeeff
AES Key Wrap in 802.11
On the next post we will dive deep in to the 4-way handshake used in a RSNA (Robust Security Network Association), during this phase the authenticator has to share the key used for multicast/broadcast transmissions, it does so by encrypting the message containing the GTK (group transient key) using AES key wrap.
Now, we finally have all the tools to deeply understand how an 802.11i RSNA works! Let’s dive into the details in the next post.
I hope this has been helpful to you!
Stay tuned for more!
Diego Capassi