In my last post, I talked about encryption modes, covering the outdated and not-so-great ECB, along with CBC and CTR. Now let’s dive into CCM (Counter with CBC-MAC), a cool encryption mode that handles both encryption and message authentication.
What makes CCM special is that it not only encrypts the data but also checks if the message has been tampered with. This check is done using something called a Message Authentication Code (MAC), or sometimes called MIC (Message Integrity Code), so it doesn’t get confused with the MAC address.
CCM is described in RFC 3610 and NIST SP 800-38C and works with 128-bit block ciphers like AES (Advanced Encryption Standard). It’s great when you need both privacy and integrity for your data.
In the 802.11i (Wi-Fi security) world, CCMP (Counter Mode with CBC-MAC Protocol) uses CCM in a specific way, with detailed info on cipher protocols, key sizes, and more. But I’ll save that for another post—stay tuned for that!
How Does CCM Work?
Basically, CCM uses CTR mode to encrypt the data, keeping it private, and CBC mode to check if the message has been tampered with, making sure it’s still intact.
In this post, I’ll show you a test vector from the 802.11 spec, proving how CCM keeps things secure and reliable.
Parameters
There are two important parameters in CCM: M and L, defined as follows:
- M: The number of bytes in the authentication field. Valid values are 4, 6, 8, 10, 12, 14, and 16. It is encoded in 3 bits using the formula:
M’ = (M / 2) – 1. - L: The number of bytes in the length field. Valid values range from 2 to 8 bytes. It is encoded in 3 bits using the formula:
L’ = L – 1.
Using a larger M increases the length of the authentication field, which adds overhead to the final encrypted data (comprising the encrypted message and the encrypted authentication value U, with a length of M). However, a larger M also reduces the likelihood of an attacker successfully modifying a message. For reference, CCMP uses M = 8 for CCMP-128 bits and M = 16 for CCMP-256.
The trade-off with L lies in its effect on the nonce length. Increasing L allows longer messages but shortens the nonce. CCMP implementations use L = 2 bytes, which balances message length and nonce size effectively.
CCM Inputs for Encryption and Authentication

- Encryption Key (K): This is the key suitable for the block cipher, such as AES with key lengths of 128, 192, or 256 bits.
- Message (m): A string of bytes where the length l(m) must satisfy the condition: 0 ≤ l(m) < 2⁸ᴸ (where L is the length field parameter defined earlier).
- AAD (Additional Authenticated Data): Data that is authenticated but not encrypted. This could include data in a header. In the CCMP implementation, AAD corresponds to parts of the 802.11 frame with certain fields zeroed out.
- Nonce (N): A “Number used Once” with a length of 15 – L bytes (recall the trade-off between L and nonce size). The nonce must be unique for each encryption operation. Reusing a nonce completely compromises the security of CCM (as explicitly warned in the RFC). In CCMP, the nonce is composed of the priority, source address (SA), and packet number.
Authentication
The overall authentication process relies on CBC (Cipher Block Chaining) mode. In CBC, the output of each encrypted block is XORed with the input of the next plaintext block. The authentication field, T, is derived from the last encrypted block.
Block Construction
The first step in the authentication process is to create the following blocks: B₀, Bₐ (AAD block), and Bₘ (message block).
Structure of B₀
The block B₀ has the following structure:
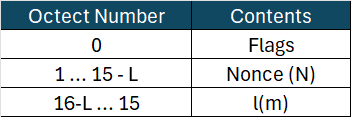
Flags Format
The flags in B₀ have the following structure
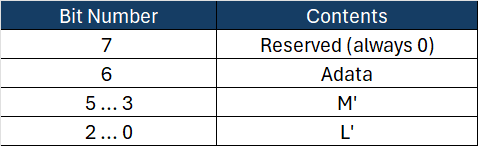
Let’s use some values to make things easier to understand.
We have the nonce (N) 005030f1844408b5039776e70c. This nonce is 13 bytes long, where its length is given by l(N) = 15 – L. Solving for L, we get L = 2.
The message (m) is f8ba1a55d02f85ae967bb62fb6cda8eb7e78a050, where l(m) is 20 bytes.
The AAD (a) is 08400fd2e128a57c5030f1844408abaea5b8fcba0000, and M is 8 bytes.
The first octet of the B₀ structure is Flags:
- The most significant bit (7) is always 0.
- Bit 6 is Adata, which indicates whether CCM has AAD. In our example, it does.
- Bits 5 to 3 represent M’, which is 2 (
011). - Bits 2 to 0 represent L’, which is 1 (
001).
The Flags octet in binary is 01011001, and in hexadecimal, it is 59.
To construct B₀, we need to add the Flags, Nonce, and the length of the message:
- Flags (hex):
59 - Nonce (N):
005030f1844408b5039776e70c - l(m): Encoded in L bytes. In this case, L = 2, so l(m) = 20 (decimal) =
0014(hex).
Thus, B₀ is:59 + 005030f1844408b5039776e70c + 0014
B₀ = 59005030f1844408b5039776e70c0014
Now, the second part is to create the AAD blocks (Bₐ) if CCM has AAD (which is always the case in CCMP).
Bₐ (not referenced as this in the RFC3610) is formed by:
- Concatenating a string that encodes l(a) with the AAD.
- Splitting this result into 16-byte blocks.
- Padding the last block with zeroes if necessary.
The process is simple, but there’s one small catch: adjusting the encoding based on the length of a.
The string encoding l(a) is created using the following rule:

In our example, the length of AAD, l(a), is 22 bytes. Since 0 < 22 < (2^16 – 2^8), l(a) is simply encoded as 0016 (22 in hex)
Next, we concatenate AAD to this encoded value:001608400fd2e128a57c5030f1844408abaea5b8fcba0000.
The result is 24 bytes. The next step is to split this into 16-byte blocks:
Bₐ = [[‘001608400fd2e128a57c5030f1844408’], [‘abaea5b8fcba00000000000000000000’]]
Since the last block only contains 8 bytes, a padding of 8 zero bytes is added to it.
Now we create the message blocks (Bₘ). This is done by splitting the message into 16-byte blocks and padding the last block with zeroes if necessary:
Bₘ = [[‘f8ba1a55d02f85ae967bb62fb6cda8eb’], [‘7e78a050000000000000000000000000’]]
The last block was padded with 12 zero bytes.
Now, we have all the blocks:
B = B₀ | Bₐ | Bₘ
B = [
[‘59005030f1844408b5039776e70c0014’],
[‘001608400fd2e128a57c5030f1844408’],
[‘abaea5b8fcba00000000000000000000’],
[‘f8ba1a55d02f85ae967bb62fb6cda8eb’],
[‘7e78a050000000000000000000000000’]
]
The process of CBC (Cipher Block Chaining) is now performed using B. We’ll use the key c97c1f67ce371185514a8a19f2bdd52f.
- The first block B₀ (
59005030f1844408b5039776e70c0014) is encrypted using the given key, resulting in the ciphertext:cd916a7eb371f0bbf472e044693cb4d2 - This ciphertext is XORed with B₁ and encrypted, producing:
072c4f129d0fdc4772fc17a14dbfc2fa - The resulting ciphertext is XORed with B₂ and encrypted, yielding:
fcd14abd11309b04b90547a0cb9d3253
The first M bytes of the last encrypted block give us T:fcd14abd11309b04
T will be used to generate U, which is the Encrypted Authentication Value. We’re almost there!
Encryption
The mode of operation for encryption is CTR (Counter) mode.
The plaintext is divided into 16-byte blocks, padded with zeroes if necessary. (This was already done with Bₘ.)
Reminder:
Bₘ = [[‘f8ba1a55d02f85ae967bb62fb6cda8eb’], [‘7e78a050000000000000000000000000’]]
Each cipher block is created by encrypting Aᵢ, where i = 0 and increments by 1 for each block.
Aᵢ has the following structure:
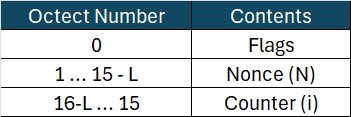
The Flags byte has the following format:
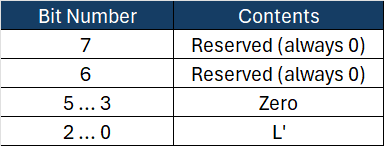
Flags is essentially L’ encoded in 3 bits. In our example, it is ‘1’ in binary, which is ’01’ in hexadecimal.
Counter i = 0
A₀ = Flags_Hex | Nonce | Counter
A₀ = 01005030f1844408b5039776e70c0000
S₀ = AES(key, A₀) = 849484b607c9ed27e704a5f44f68f86′
A1 = 01005030f1844408b5039776e70c0001
S₁ = AES(key, A₁) = 0b6ab8ab4a123a8dd4ddf5cb848b40e7
A2 = 01005030f1844408b5039776e70c0002
S₂ = AES(key, A₂) = 427c7049bf6b207e867bf76eb339c728
S₀ is used to create the Encrypted Authentication Value (U):
U = XOR(S₀, T)
S₀ needs to be truncated to match the number of bytes of T.
T = fcd14abd11309b04
U = fcd14abd11309b04 XOR fcd14abd11309b04
U = 7845ce0b16f97623
We now have the Encrypted Authentication Value (U)!
To encrypt the data, it is only necessary to XOR each block Bₘ with the respective Sᵢ block, starting from S₁.
Eᵢ = Bₘᵢ XOR Sᵢ (Remove the padding if necessary and truncate Bₘᵢ to match the number of bytes of Sᵢ).
The first encrypted message block is:
E₁ = f8ba1a55d02f85ae967bb62fb6cda8eb XOR 0b6ab8ab4a123a8dd4ddf5cb848b40e7, which results in f3d0a2fe9a3dbf2342a643e43246e80c.
For i = 1 to the number of blocks:
E₂ = 7e78a050 XOR 427c7049
E₂ = 3c04d019
Concatenating E₁ with E₂, we get:
f3d0a2fe9a3dbf2342a643e43246e80c3c04d019
This is the output of CCM:
- Encrypted Message (c) = f3d0a2fe9a3dbf2342a643e43246e80c3c04d019
- Encrypted Authentication Value (U) = 7845ce0b16f97623
The encrypted and authenticated message (C) is:
f3d0a2fe9a3dbf2342a643e43246e80c3c04d0197845ce0b16f97623
Decryption and Authentication Checking
The required inputs for decryption and authentication checking are:
- Encryption key (K)
- Nonce (n)
- AAD (a)
- The encrypted and authenticated message (C)
The decryption process is very similar to the encryption process. The first step is to recover the message and the MAC value T.
To extract U from the encrypted and authenticated message, we get U = 7845ce0b16f97623. Next, we encrypt A₀ (with the counter set to 0) and XOR the result with U to retrieve T, which is fcd14abd11309b04.
As mentioned earlier in the CTR mode post, the decryption process is the same as encryption. The only difference is that we input the ciphertext and get the plaintext as the output. This is because the process relies on encrypting the counter, not the message. The message is XORed with the encrypted counter. The counter Aₙ is obtained using the process described earlier and encrypted to create Sₙ.
Sₙ will be the same. Essentially, we’re doing a XOR between the ciphertext output and the counter, which will result in the message:
m₁ = E₁ XOR S₁
m₁ = f3d0a2fe9a3dbf2342a643e43246e80c XOR 0b6ab8ab4a123a8dd4ddf5cb848b40e7
m₁ = f8ba1a55d02f85ae967bb62fb6cda8eb
m₂ = E₂ XOR S₂
m₂ = 3c04d019 XOR 427c7049
m₂ = 7e78a050
Concatenating m₁ and m₂, we get:
m = f8ba1a55d02f85ae967bb62fb6cda8eb7e78a050
The receiver has the AAD in order to compute the authentication check, using the message as well, the same process is repeated as described in the Authentication section, computing CBC and getting the value fcd14abd11309b04, which guarantees the data integrity. The data is authenticated because, using only the key, we were able to generate the code U.
This test vector was derived from the test vector values specified in the IEEE 802.11 specification.
As I mentioned, CCMP is an implementation of CCM, with additional specifications for how certain elements are handled. Specifically, it defines the use of AES in CTR mode for encryption, along with how the AAD (Additional Authenticated Data), nonce, and MIC (Message Integrity Code) length are managed. The MIC length is 8 bytes for CCMP-128 and 16 bytes for CCMP-256.
In a future post, I’ll dive deeper into these details and show how real packet encryption and decryption work in practice. I’ll also take a closer look at the encryption keys used in the CCMP process.
Additionally, stay tuned for a post on GCM (Galois/Counter Mode), another mode that builds on counter-based encryption and is implemented using GCMP (WPA-3).
I hope this explanation was useful—more content coming soon!
Diego Capassi
References
https://datatracker.ietf.org/doc/html/rfc3610
IEEE Std 802.11 Working Group, IEEE Std 802.11. Wireless LAN. Medium Access Control (MAC) and Physical Layer (PHY). Specifications of IEEE 802.11

