WPA3 uses advanced encryption techniques to protect data confidentiality and integrity in wireless networks. The encryption method it uses is Galois/Counter Mode (GCM), which enhances security by providing both encryption and authentication efficiently.
Let’s take a closer look at GCM, the encryption mode used in WPA3!
In my previous post, I explained the CCM process, a cipher mode that combines CTR for confidentiality and CBC for authentication. CCMP, the implementation of CCM, is used in WPA2. Like CCM, GCM offers both encryption and authentication, but with some important differences.
GCM Inputs/Outputs

Secret key (K): Matches the block cipher algorithm. For AES, it can be 128, 192, or 256 bits.
Initialization vector (IV) ,Can range from 1 to 124 bits. However, a 96-bit IV makes the algorithm more efficient (we’ll explain why later).
Plaintext (P), Ranges between 0 and 239 − 256 bits.
Additional authenticated data (AAD), (A). Data that is authenticated but not encrypted. It can be any size between 0 and 264 bits, typically used for headers or contextual information.
The building blocks
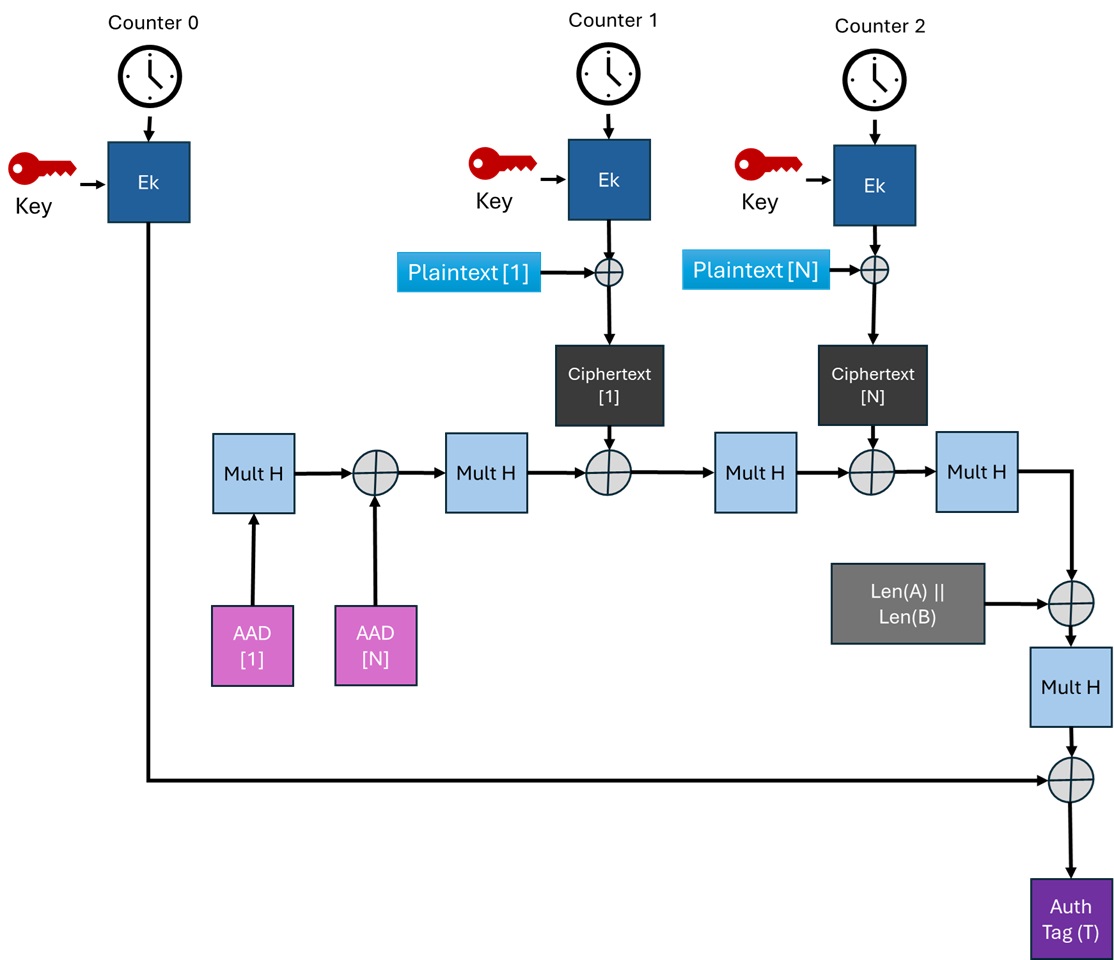
Encryption
GCM uses CTR mode for encryption. In this process, the ‘Counter’ is encrypted, and the result is XORed with the plaintext to generate the ciphertext.
In the specification, this operation is described as:
- Y0 = IV || 31 zeros || 1 (This is only true for IV with lenght of 96 bits, more about it later)
- Yi = incr(Yi−1) for i = 1, . . . , n (1)
- Ci = Pi ⊕ E(K, Yi) for i = 1, . . . , n − 1
Y0 can be seen as the counter or nonce where the index is 0, and it is used in the final part of the process to generate the authentication tag.
Y1 through Yn represent the counters used during encryption.
The last block of plaintext doesn’t need to be 128 bits, since CTR is a stream cipher. We only need to take the most significant bits from the output of the encryption of the counter, match the length of the plaintext, and XOR it with the plaintext.
- C∗ = P∗ ⊕ MSBu(E(K, Yn))
where the number of bits in the final block C∗ is u
Finite Field multiplication
This section dives into the details of the operation. If you’re not into the nitty-gritty, feel free to skip ahead!
The authentication process of the GCM relies on operations with blocks created from AAD, CiperText, length of A and C and the Counter, this operations is the multiplication of the values with H in Galois Field (2128) which results in values of 128 bits.
On the AES post i talked a little about Galois multiplication, but it was a field with less elements GF(28).
The same logic holds here, we treat the values as a polynomial, let’s says we want to multiply:
a = x127
b = x127+1
a * b = x127 ( x127+1)
a * b = x254+x127
This result has (x254) the element which is not in the finite field of GF(x128), so we have to divided it by the irreducible polynomial defined in the standard: P(x) = x128+x7+x2+x+1, the remainder is the result.
x254 is the highest degree, we have to find an element of the field, which multiplied by P(x) and XORed (subtracted) with this term is going to cancel it. The answer is x126. So x126*P(x) = x254+x133+x128+x127+x126. doing the XOR with x254+x127 we get:
x133+x128+x126 ,this is not in the field, so let’s keep dividing.
The highter term is (x133), let’s reduce the degree, x5 * P(x) = x133+x12+x7+x6+x5. Doing the XOR we get:
x128+x126+x12+x7+x6+x5 almost there, but we need to reduce it again.
To reduce highest element (x128) we need to multiply P(x) by 1 and XOR it again, we we get:
x126+x12+x6+x5+x2+x+1 . This is part of the GF(2128), it is the remainder of division.
Doing this process manually is cumbersome but this is a very straightforward to be done by computers.
Authentication
The process to create the authentication tag begins by creating H, which is the cipertext generated by encrypting 128 zero bits.
H = E(K, 0128)
The ‘Mult H’ block on the diagram does the multiplication as described (but in little endian, e.g: ‘1001001’ is 1+x3+x6.
The authentication process generates T, where:
T = MSBt(GHASH(H, A, C) ⊕ E(K, Y0))
GHASH(H, A, C) = Xm+n+1
GHASH(H, A, C) is the function which received H, A (AAD) and the C, Ciphertext.

The Additional Authenticated Data (AAD) is combined with the previous value by performing an XOR operation and then multiplying the result by the hash key, H.
(Xi−1 ⊕ Ai) · H for i = 1, . . . , m − 1
The last block of Additional Authenticated Data (AAD), labeled Am, is padded with zeros to the appropriate length and then multiplied by the hash key, H.
(Xm−1 ⊕ (A∗ m || 0128-v)) · H for i = m
After processing the AAD, the same process is applied to the Ciphertext. Each Ciphertext block is XORed with the previous result and then multiplied by the hash key, H.
The final block of Ciphertext is padded with zeros until it reaches 128 bits before being processed.
(Xm+n−1 ⊕ (Cm∗ || 0128-u)) · H
The final step is to XOR the lengths of the Additional Authenticated Data (LenA) and the Ciphertext (LenC), with both lengths encoded as 64-bit values. This result is then multiplied by the hash key, H, producing the GHASH output.
The authentication tag is created by XORing the encrypted initial counter block (Counter 0 or Y0) with the GHASH output.
The most significant bits of this result are extracted based on the desired length of the authentication tag.
T = MSBt(GHASH(H, A, C) ⊕ E(K, Y0))
That’s enough theory—now let’s dive in and encrypt some data using GCM!
Input
K = feffe9928665731c6d6a8f9467308308
P= [‘d9313225f88406e5a55909c5aff5269a’,’86a7a9531534f7da2e4c303d8a318a72′,’1c3c0c95956809532fcf0e2449a6b525′,’b16aedf5aa0de657ba637b39′]
A (AAD) = feedfacedeadbeeffeedfacedeadbeefabaddad2
IV = cafebabefacedbaddecaf888
Encryption
The first step for encryption is to calculate Y0. If the Initialization Vector (IV) is 96 bits long, the rule is:
Y0 = IV || 31 zeros || 1 [ IV in binary]
Y0 = cafebabefacedbaddecaf88800000001
Yn = Y0 + n
We have four blocks of plaintext to encrypt, so we will use Y1, Y2, Y3, and Y4 as the counter blocks.
The table below shows the result of each encrypted block. Notice that the last block is shorter than 128 bits, so it is padded with zeros before performing the XOR operation:

The ciphertext C is obtained by concatenating the result of each encrypted block
42831ec2217774244b7221b784d0d49ce3aa212f2c02a4e035c17e2329aca12e21d514b25466931c7d8f6a5aac84aa051ba30b396a0aac973d58e091
Authentication
The first step to create the authentication Tag is calculate H, which is H = E(K, 0128).
H = b83b533708bf535d0aa6e52980d53b78.
Now we will do the GHASH(H, A, C) process.
The simplest approach I found was to first create the data blocks using A (AAD) and the ciphertext (C), adding padding if needed.
A = feedfacedeadbeeffeedfacedeadbeefabaddad2 it has 160 bits, we will have to pad it to be a multiple of 128, adding 96 zero bits.
A_padded = feedfacedeadbeeffeedfacedeadbeefabaddad2000000000000000000000000
C has 480 bits, so we need to add 32 bits to complete the block.
42831ec2217774244b7221b784d0d49ce3aa212f2c02a4e035c17e2329aca12e21d514b25466931c7d8f6a5aac84aa051ba30b396a0aac973d58e09100000000.
The last block will contain the length of the Additional Authenticated Data (AAD) and the length of the Ciphertext (C), each encoded as 64-bit values.
For A, which is 160 bits, the length is encoded as a0 in hexadecimal.
For C, which is 480 bits, the length is encoded as 1e0 in hexadecimal.
When concatenated and encoded, we get:
00000000000000a000000000000001e0
Now lets create the 128 bits blocks
Blocks =
[
‘feedfacedeadbeeffeedfacedeadbeef’,
‘abaddad2000000000000000000000000’,
‘42831ec2217774244b7221b784d0d49c’,
‘e3aa212f2c02a4e035c17e2329aca12e’,
’21d514b25466931c7d8f6a5aac84aa05′,
‘1ba30b396a0aac973d58e09100000000’,
‘00000000000000a000000000000001e0’
]
Now, the process is to XOR each block with the previous result, starting with zero, and then multiply the result by H.

The output is the GHASH, 698e57f70e6ecc7fd9463b7260a9ae5f.
The last step is to XOR with the E(k,Y0)
E(k,Yn) = 3247184b3c4f69a44dbcd22887bbb418
T = 3247184b3c4f69a44dbcd22887bbb418 XOR 698e57f70e6ecc7fd9463b7260a9ae5f
T = 5bc94fbc3221a5db94fae95ae7121a47
Finally, we obtain the authentication tag. This tag is sent along with the ciphertext so that the receiver can decrypt the packet and verify the tag. If any bit in the ciphertext or AAD changes, the tag will also change, allowing the receiver to detect any tampering!
The output of CGM is:
Ciphertext (C) = 42831ec2217774244b7221b784d0d49ce3aa212f2c02a4e035c17e2329aca12e21d514b25466931c7d8f6a5aac84aa051ba30b396a0aac973d58e091
Authentication Tag (T) = 5bc94fbc3221a5db94fae95ae7121a47

The results match exactly with the data from test vector number 4 of the NIST document, reference [1], which was used as the input.
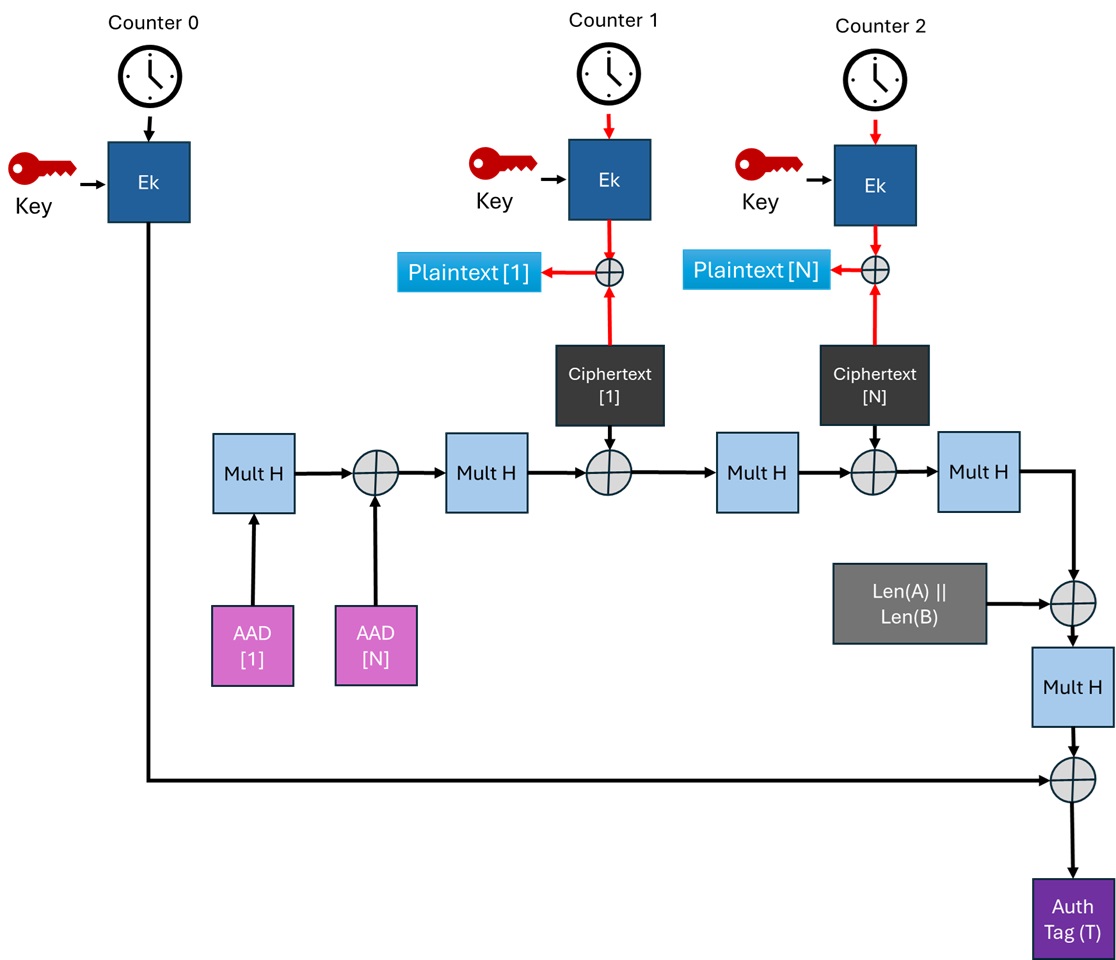
Decryption
The decryption process is based on the same principles as CTR mode. Since the plaintext is not directly encrypted, the receiver calculates the counters, encrypts them, and then XORs the result with the ciphertext to retrieve the plaintext blocks. The authentication process uses the received ciphertext to verify if the authentication tag matches the one calculated by the receiver.
Performance
GCM is more efficient than CCM because it enables better performance, including the ability to parallelize certain operations.
The benchmark below was conducted using the python Crypto library, comparing 5000 encrypt/decrypt processes with CCM and GCM. The results show that GCM was 58% faster for encryption and 67% faster for decryption on average.
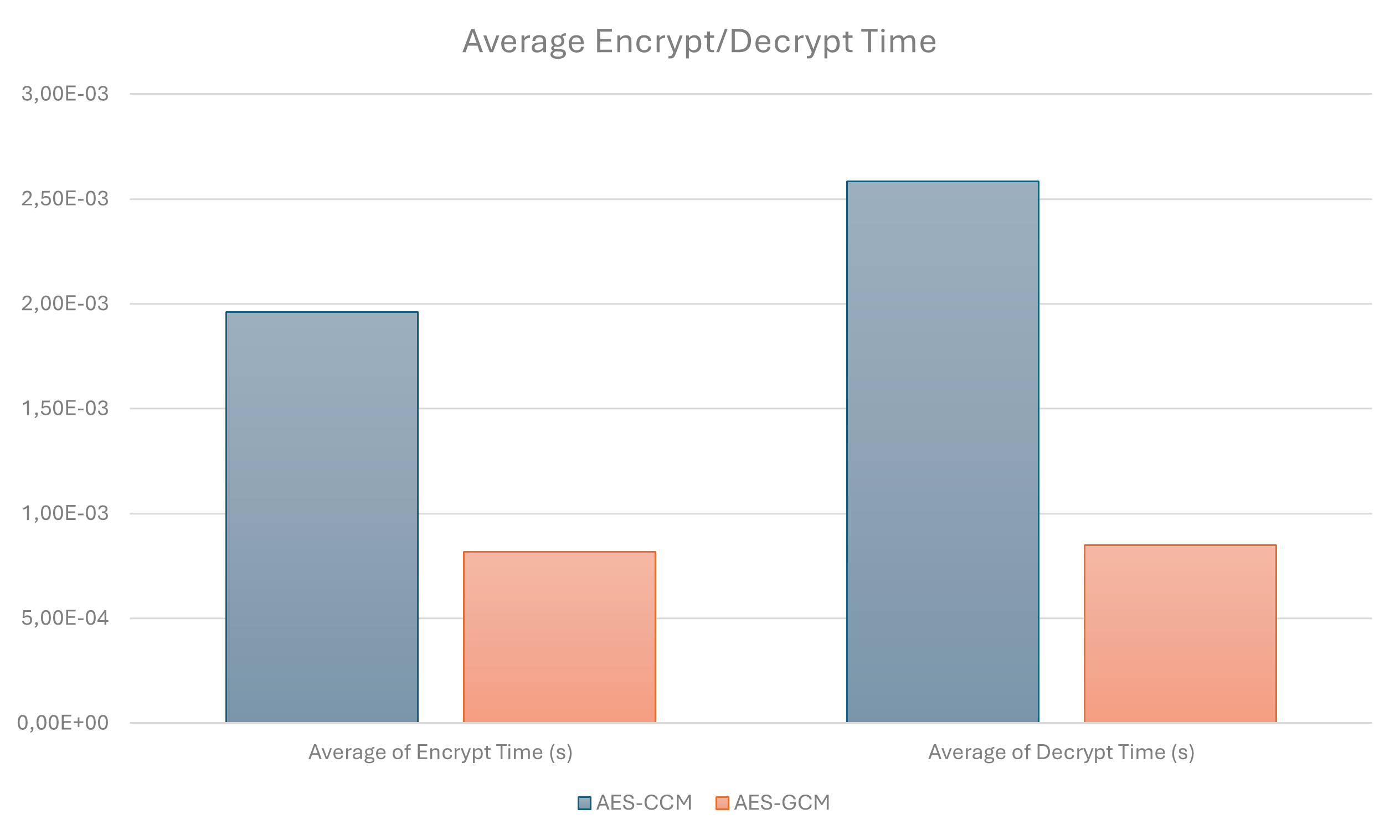
Final thoughts:
If the IV is not 96 bits, the process to create the IV is GHASH}(H, {}, {IV}). This essentially creates a 128-bit block using the IV and applies the sequence of XOR operations, multiplying by H. Don’t forget to include the last block with the length of the AAD and Ciphertext.
The length of the Authentication Tag is defined in the NIST Standard 800-38D as 128, 120, 112, 104, or 96 bits. In some applications, it may also be 64 or 32 bits.
GCM defines a generic authenticated encryption mode, while GCMP is the 802.11 implementation of GCM that specifies the encryption protocol (AES), key length, rules for creating AAD, and the IV (nonce), tag length (128 bits).
That’s it! I hope you enjoyed it! For me, at least, it was a great learning experience.
Stay tuned,
Diego Capassi
References
[1] D. McGrew, J. Viega, The Galois/Counter Mode of Operation (GCM), Natl. Inst. Stand.
Technol. [Web page], http://www.csrc.nist.gov/groups/ST/toolkit/BCM/documents/
proposedmodes/gcm/gcm-revised-spec.pdf, May 31, 2005.
National Institute of Standards and Technology (NIST), Special Publication 800-38D: Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC, NIST, 2007. [Online]. Available: https://doi.org/10.6028/NIST.SP.800-38D
IEEE Standard 802.11-2016, “IEEE Standard for Information technology—Local and metropolitan area networks—Specific requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications,”
